Which of the Following Mathematical Operations Can Be Used With Functions? Select All That Apply.

Learning Outcomes

• Combine functions using algebraic operations.
• Create a new function by composition of functions.

Function limerick is only one way to combine existing functions. Some other way is to behave out the usual algebraic operations on functions, such equally addition, subtraction, multiplication and division. Nosotros exercise this past performing the operations with the role outputs, defining the result as the output of our new part.

Suppose nosotros need to add two columns of numbers that represent a husband and wife's split annual incomes over a flow of years, with the issue being their total household income. We want to do this for every twelvemonth, adding simply that twelvemonth's incomes and so collecting all the data in a new column. If [latex]west\left(y\correct)[/latex] is the wife's income and [latex]h\left(y\right)[/latex] is the husband's income in year [latex]y[/latex], and nosotros want [latex]T[/latex] to correspond the total income, then we can define a new function.

[latex]T\left(y\correct)=h\left(y\correct)+w\left(y\right)[/latex]

If this holds true for every year, then we can focus on the relation betwixt the functions without reference to a yr and write

[latex]T=h+due west[/latex]

Just as for this sum of two functions, nosotros tin define divergence, product, and ratio functions for whatever pair of functions that have the same kinds of inputs (not necessarily numbers) and also the same kinds of outputs (which do have to be numbers so that the usual operations of algebra can apply to them, and which also must have the same units or no units when we add and subtract). In this way, we can retrieve of adding, subtracting, multiplying, and dividing functions.

For two functions [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)[/latex] with real number outputs, we ascertain new functions [latex]f+g,f-g,fg[/latex], and [latex]\dfrac{f}{g}[/latex] past the relations

[latex]\brainstorm{align}{c}\left(f+thou\right)\left(ten\right)&=f\left(x\right)+thousand\left(x\right) \\[2mm] \left(f-g\right)\left(x\right)&=f\left(x\right)-g\left(ten\correct) \\[2mm] \text{ }\left(fg\right)\left(ten\correct)&=f\left(10\correct)thousand\left(x\correct) \\[2mm] \text{ }\left(\dfrac{f}{g}\right)\left(x\correct)&=\dfrac{f\left(x\right)}{grand\left(10\right)}\\& \stop{align}[/latex]

Example: Performing Algebraic Operations on Functions

Find and simplify the functions [latex]\left(k-f\right)\left(x\right)[/latex] and [latex]\left(\dfrac{g}{f}\right)\left(10\right)[/latex], given [latex]f\left(10\right)=10 - i[/latex] and [latex]g\left(x\right)={x}^{two}-1[/latex]. Requite the domain of your event. Are they the aforementioned function?

Endeavor It

Find and simplify the functions [latex]\left(fg\right)\left(x\right)[/latex] and [latex]\left(f-thousand\right)\left(x\right)[/latex].

[latex]f\left(x\right)=x - ane\text{ and }g\left(x\correct)={x}^{ii}-1[/latex]

Are they the same office?

Try It

Allow'southward explore what happens to the graphs of functions that are combined using algebraic operations. Use an online graphing tool to graph the following functions:

1. [latex]f(x) = x^2+3x-four[/latex]
2. [latex]k(x) = \dfrac{1}{10-one}[/latex]

At present, enter [latex]h(x) = f(10)+g(ten)[/latex] into the next line.

Evaluate [latex]h(1)[/latex], why practise you recall you lot get this outcome?

Create a New Function Using a Composition

Performing algebraic operations on functions combines them into a new function, but we tin can too create functions by composing functions. When we wanted to compute a heating cost from a solar day of the year, we created a new function that takes a mean solar day as input and yields a cost as output. The process of combining functions so that the output of one function becomes the input of some other is known every bit a composition of functions. The resulting function is known every bit a composite part. We correspond this combination past the post-obit note:

[latex]\left(f\circ 1000\right)\left(x\right)=f\left(g\left(10\right)\right)[/latex]

We read the left-hand side every bit [latex]``f[/latex] composed with [latex]m[/latex] at [latex]x,''[/latex] and the right-hand side as [latex]``f[/latex] of [latex]one thousand[/latex] of [latex]x.''[/latex] The 2 sides of the equation take the same mathematical meaning and are equal. The open circle symbol [latex]\circ [/latex] is called the composition operator. We use this operator mainly when we wish to emphasize the relationship betwixt the functions themselves without referring to whatever detail input value. Composition is a binary performance that takes two functions and forms a new function, much as addition or multiplication takes two numbers and gives a new number. However, it is important non to confuse function composition with multiplication because, as we learned above, in most cases [latex]f\left(thou\left(x\right)\correct)\ne f\left(ten\correct)1000\left(ten\right)[/latex].

Information technology is too of import to empathise the society of operations in evaluating a blended part. We follow the usual convention with parentheses past starting with the innermost parentheses first, and then working to the exterior. In the equation higher up, the function [latex]g[/latex] takes the input [latex]x[/latex] start and yields an output [latex]g\left(ten\correct)[/latex]. Then the function [latex]f[/latex] takes [latex]thousand\left(x\right)[/latex] as an input and yields an output [latex]f\left(g\left(10\right)\right)[/latex].

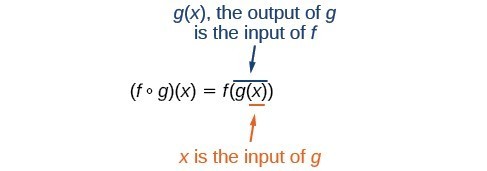
Figure 2

In general [latex]f\circ grand[/latex] and [latex]k\circ f[/latex] are different functions. In other words in many cases [latex]f\left(g\left(x\right)\correct)\ne g\left(f\left(x\right)\right)[/latex] for all [latex]x[/latex].

For case if [latex]f\left(10\right)={10}^{2}[/latex] and [latex]thousand\left(x\correct)=x+2[/latex], and then

[latex]\begin{align}f\left(g\left(10\right)\right)&=f\left(x+2\right) \\[2mm] &={\left(x+2\correct)}^{two} \\[2mm] &={x}^{two}+4x+4\hfill \end{marshal}[/latex]

but

[latex]\brainstorm{align}g\left(f\left(x\right)\right)&=g\left({x}^{2}\right) \\[2mm] \text{ }&={x}^{ii}+2\hfill \finish{align}[/latex]

These expressions are non equal for all values of [latex]10[/latex], then the two functions are not equal. Information technology is irrelevant that the expressions happen to be equal for the single input value [latex]x=-\frac{ane}{2}[/latex].

Note that the range of the inside office (the first function to be evaluated) needs to be within the domain of the outside function. Less formally, the composition has to brand sense in terms of inputs and outputs. Additionally, in applied settings, function composition normally only makes sense in ane specific order.

A General Note: Composition of Functions

When the output of one function is used equally the input of another, we call the entire operation a composition of functions. For whatsoever input [latex]x[/latex] and functions [latex]f[/latex] and [latex]thou[/latex], this action defines a blended function, which we write equally [latex]f\circ grand[/latex] such that

[latex]\left(f\circ m\right)\left(ten\right)=f\left(g\left(ten\right)\correct)[/latex]

The domain of the blended function [latex]f\circ k[/latex] is all [latex]x[/latex] such that [latex]x[/latex] is in the domain of [latex]g[/latex] and [latex]g\left(x\right)[/latex] is in the domain of [latex]f[/latex].

It is important to realize that the product of functions [latex]fg[/latex] is non the same every bit the function composition [latex]f\left(k\left(ten\right)\right)[/latex], considering, in general, [latex]f\left(ten\right)g\left(ten\right)\ne f\left(g\left(x\right)\right)[/latex].

Instance: Ascertain a Composition of Functions

Using the functions provided, find [latex]f\left(g\left(x\right)\correct)[/latex] and [latex]g\left(f\left(10\right)\correct)[/latex].
[latex]f\left(10\correct)=2x+i\\g\left(10\right)=three-x[/latex]

Try It

At present we will explore the graph of a limerick of functions. Use an online graphing tool to graph the post-obit functions:

1. [latex]f(x) = ten^2+3x-iv[/latex]
2. [latex]g(x) = \dfrac{1}{10-1}[/latex]

Now define a new function:

[latex]h(ten) = f(f(x))[/latex]

Now zoom in (utilize the plus sign in the upper right-paw corner of the graph) on the point [latex](0.23607,-3.236)[/latex], find that both graphs pass through this point. Continue this design for a few more than iterations: define a new office that contains some other composition of [latex]f(x)[/latex] with itself. For example: [latex]p(x) = f(f(f(x)))[/latex], and then on. Continue to use the zoom as you iterate.

The indicate [latex](0.23607,-iii.236)[/latex] is called a fixed point of the part [latex]f(x)=x^2+3x-four[/latex]. Stock-still points are used in mathematical applications such every bit the page rank algorithm that Google uses to generate internet search results. Read more than near fixed points hither, and folio rank here.

Example: Interpreting Composite Functions

The function [latex]c\left(s\right)[/latex] gives the number of calories burned completing [latex]s[/latex] sit down-ups, and [latex]s\left(t\right)[/latex] gives the number of sit-ups a person can consummate in [latex]t[/latex] minutes. Interpret [latex]c\left(s\left(three\right)\right)[/latex].

Example: Investigating the Order of Role Composition

Suppose [latex]f\left(x\right)[/latex] gives miles that tin exist driven in [latex]10[/latex] hours and [latex]yard\left(y\correct)[/latex] gives the gallons of gas used in driving [latex]y[/latex] miles. Which of these expressions is meaningful: [latex]f\left(grand\left(y\right)\correct)[/latex] or [latex]grand\left(f\left(10\right)\right)?[/latex]

Endeavour It

Q & A

Are there whatsoever situations where [latex]f\left(g\left(y\correct)\right)[/latex] and [latex]yard\left(f\left(10\correct)\right)[/latex] would both be meaningful or useful expressions?

Yes. For many pure mathematical functions, both compositions make sense, even though they usually produce different new functions. In real-world problems, functions whose inputs and outputs accept the same units as well may give compositions that are meaningful in either gild.

Try Information technology

The gravitational forcefulness on a planet a distance [latex]r[/latex] from the sun is given by the office [latex]G\left(r\right)[/latex]. The dispatch of a planet subjected to any strength [latex]F[/latex] is given past the office [latex]a\left(F\right)[/latex]. Course a meaningful composition of these 2 functions, and explicate what it means.

Show Show Solution

A gravitational force is still a force, then [latex]a\left(One thousand\left(r\right)\correct)[/latex] makes sense as the acceleration of a planet at a altitude r from the Sun (due to gravity), but [latex]Chiliad\left(a\left(F\right)\right)[/latex] does non brand sense.

Contribute!

Did you have an idea for improving this content? We'd love your input.

Improve this pageLearn More

petersonbonly1984.blogspot.com

Source: https://courses.lumenlearning.com/waymakercollegealgebra/chapter/compositions-of-functions/

Share this post